Publications

Spotlight

Metropolis-Hastings (MH) is a commonly-used MCMC algorithm, but it can be intractable on large datasets due to requiring computations over the whole dataset. In this paper, we study minibatch MH methods, which instead use subsamples to enable scaling. We observe that most existing minibatch MH methods are inexact (i.e. they may change the target distribution), and show that this inexactness can cause arbitrarily large errors in inference. We propose a new exact minibatch MH method, TunaMH, which exposes a tunable trade-off between its minibatch size and its theoretically guaranteed convergence rate. We prove a lower bound on the batch size that any minibatch MH method must use to retain exactness while guaranteeing fast convergence—the first such bound for minibatch MH—and show TunaMH is asymptotically optimal in terms of the batch size. Empirically, we show TunaMH outperforms other exact minibatch MH methods on robust linear regression, truncated Gaussian mixtures, and logistic regression.

Ruqi Zhang*, A. Feder Cooper*, Christopher De Sa

Advances in Neural Information Processing Systems 33 pre-proceedings (NeurIPS 2020)

Spotlight

Many learning algorithms, such as stochastic gradient descent, are affected by the order in which training examples are used. It is often observed that sampling the training examples without replacement, also known as random reshuffling, causes learning algorithms to converge faster. We give a counterexample to the Operator Inequality of Noncommutative Arithmetic and Geometric Means, a longstanding conjecture that relates to the performance of random reshuffling in learning algorithms (Recht and Ré, “Toward a noncommutative arithmetic-geometric mean inequality: conjectures, case-studies, and consequences,” COLT 2012). We use this to give an example of a learning task and algorithm for which with-replacement random sampling actually outperforms random reshuffling.

Christopher De Sa

Advances in Neural Information Processing Systems 33 pre-proceedings (NeurIPS 2020)

Spotlight

Hyperbolic embeddings achieve excellent performance when embedding hierarchical data structures like synonym or type hierarchies, but they can be limited by numerical error when ordinary floating-point numbers are used to represent points in hyperbolic space. Standard models such as the Poincaré disk and the Lorentz model have unbounded numerical error as points get far from the origin. To address this, we propose a new model which uses an integer-based tiling to represent any point in hyperbolic space with provably bounded numerical error. This allows us to learn high-precision embeddings without using BigFloats, and enables us to store the resulting embeddings with fewer bits. We evaluate our tiling-based model empirically, and show that it can both compress hyperbolic embeddings (down to 2% of a Poincaré embedding on WordNet Nouns) and learn more accurate embeddings on real-world datasets.

Tao Yu, Christopher M. De Sa

Advances in Neural Information Processing Systems 32 (NeurIPS 2019)

Spotlight

Gibbs sampling is a Markov chain Monte Carlo method that is often used for learning and inference on graphical models. Minibatching, in which a small random subset of the graph is used at each iteration, can help make Gibbs sampling scale to large graphical models by reducing its computational cost. In this paper, we propose a new auxiliary-variable minibatched Gibbs sampling method, Poisson-minibatching Gibbs, which both produces unbiased samples and has a theoretical guarantee on its convergence rate. In comparison to previous minibatched Gibbs algorithms, Poisson-minibatching Gibbs supports fast sampling from continuous state spaces and avoids the need for a Metropolis-Hastings correction on discrete state spaces. We demonstrate the effectiveness of our method on multiple applications and in comparison with both plain Gibbs and previous minibatched methods.

Ruqi Zhang, Christopher M. De Sa

Advances in Neural Information Processing Systems 32 (NeurIPS 2019)

Long Oral

In distributed statistical learning, N samples are split across m machines and a learner wishes to use minimal communication to learn as well as if the examples were on a single machine. This model has received substantial interest in machine learning due to its scalability and potential for parallel speedup. However, in high-dimensional settings, where the number examples is smaller than the number of features (“dimension”), the speedup afforded by distributed learning may be overshadowed by the cost of communicating a single example. This paper investigates the following question: When is it possible to learn a d-dimensional model in the distributed setting with total communication sublinear in d? Starting with a negative result, we observe that for learning ℓ1-bounded or sparse linear models, no algorithm can obtain optimal error until communication is linear in dimension. Our main result is that by slightly relaxing the standard boundedness assumptions for linear models, we can obtain distributed algorithms that enjoy optimal error with communication logarithmic in dimension. This result is based on a family of algorithms that combine mirror descent with randomized sparsification/quantization of iterates, and extends to the general stochastic convex optimization model.

Jayadev Acharya, Chris De Sa, Dylan Foster, Karthik Sridharan

Proceedings of the 36th International Conference on Machine Learning (ICML 2019)

Long Oral

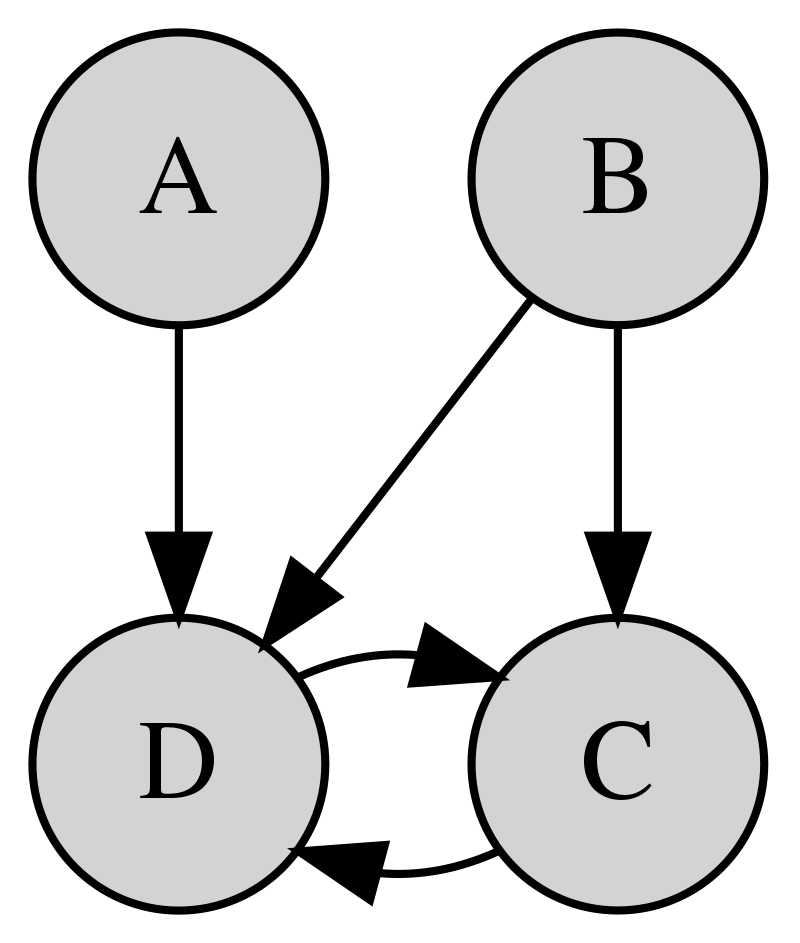
Gibbs sampling is the de facto Markov chain Monte Carlo method used for inference and learning on large scale graphical models. For complicated factor graphs with lots of factors, the performance of Gibbs sampling can be limited by the computational cost of executing a single update step of the Markov chain. This cost is proportional to the degree of the graph, the number of factors adjacent to each variable. In this paper, we show how this cost can be reduced by using minibatching: subsampling the factors to form an estimate of their sum. We introduce several minibatched variants of Gibbs, show that they can be made unbiased, prove bounds on their convergence rates, and show that under some conditions they can result in asymptotic single-update-run-time speedups over plain Gibbs sampling.

Chris De Sa, Vincent Chen, Wing Wong

Proceedings of the 35th International Conference on Machine Learning (ICML 2018)

Long Oral

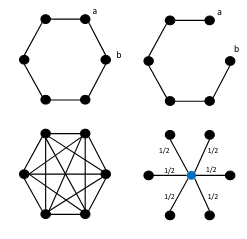
Hyperbolic embeddings offer excellent quality with few dimensions when embedding hierarchical data structures. We give a combinatorial construction that embeds trees into hyperbolic space with arbitrarily low distortion without optimization. On WordNet, this algorithm obtains a mean-average-precision of 0.989 with only two dimensions, outperforming existing work by 0.11 points. We provide bounds characterizing the precision-dimensionality tradeoff inherent in any hyperbolic embedding. To embed general metric spaces, we propose a hyperbolic generalization of multidimensional scaling (h-MDS). We show how to perform exact recovery of hyperbolic points from distances, provide a perturbation analysis, and give a recovery result that enables us to reduce dimensionality. Finally, we extract lessons from the algorithms and theory above to design a scalable PyTorch-based implementation that can handle incomplete information.

Frederic Sala, Christopher De Sa, Albert Gu, Christopher Ré

Proceedings of the 35th International Conference on Machine Learning (ICML 2018)